Take a look at this drawing of a fern:

It looks complicated, right? Like it was drawn by an artist or traced from a real plant. If I asked you to come up with a procedure for generating this shape, you might not know where to start.

Surprisingly, this fern structure is generated by running a simple procedure on a small set of information. It won't make sense to you yet, but this is the set of information that generates the fern shape:

This shape and the rules that generate it are an example of a mathematical structure called an L-system, or Lindenmayer system, named after the Hungarian biologist who developed them to simulate plant growth. In this post, we will begin by uncovering the inner workings and beauty of L-systems. Then we will dive deeper into the world of pure mathematics, exploring the idea of choosing a set of information to generate a "picture" of a mathematical theory. Don't worry if this doesn't make sense yet, we'll take it one step at a time. Let's dive right in!

L-Systems

Have you ever used the find-and-replace tool in a code editor or word processor? Because find-and-replace is exactly the procedure that makes L-systems grow. We start with some initial symbol (which we call the axiom) and repeatedly find certain patterns and replace them with other patterns, according to our given rules. As we do this, we generate an increasingly long and complex string of symbols. Let's take a look at an example to make this clearer.

rule1 means find all occurrences of A and replace them with AB.

rule2 means find all occurrences of B and replace them with A.

Using this set of information which specifies an L-system, this is how we use find-and-replace to grow it:

At this point, you might be wondering how this process of generating strings of symbols like ABAABABA has anything to do with generating elegant shapes like the fern. Let's take a look at another example to answer this question.

Note that F, G, +, and − are being used as symbols here, just the same as A and B from before. In particular, + and − have no mathematical significance in this context. When we grow a string using the find-and-replace procedure on this new axiom and rules, we obtain the following:

Here is an animation to help illustrate what's going on here:

The long string of symbols that we create through this process doesn't appear particularly appealing to the eye—it just looks like a mess. But there is a way to give this messy string a visual interpretation which reveals its complex structure.

Let's imagine that our string is a set of instructions for a robot illustrator. We will associate each symbol in the string with an instruction to our robot. For example, let's say that F and G both mean draw forward. And let's say that + means turn left 90°, while − means turn right 90°. Now to transform our string into a picture, we give it to the robot who reads it symbol by symbol, following the instructions one at a time. When we ask the robot illustrator to draw using the string we generated above at iteration 10, this picture emerges:

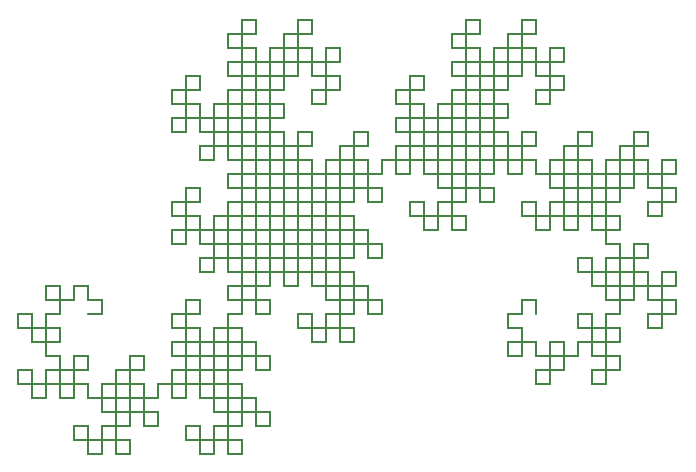
If you don't believe me, try being the robot illustrator yourself and follow the instructions on a piece of paper!

Phew! That was a lot of information so let's summarize. An L-system has an initial symbol called an axiom and a set of find-and-replace rules. We start from the axiom and follow the rules to find and replace symbols over multiple iterations, generating a long and messy string of symbols. Finally, we give each symbol a visual interpretation (like draw forward, turn right 90°, etc.) to transform the string into a picture that reveals the complexity and beauty hidden within the mess. And remember the fern shape from the beginning? That fern is the L-system generated by the following axiom and rules...

...where F means draw forward, r means turn right 25°, and l means turn left 25°. What about the bracket symbols, ] and [? The opening bracket [ means "store the current position and direction for later", and the closing bracket ] means "restore the most recent position and direction that was stored". For those familiar with stack data structures, we might call these operations push and pop. What about the symbol X? X has no visual interpretation, but it's still an important symbol for the growth of the L-system, since it appears in rule1. This is how the fern is generated. I think it's amazing that the beautiful, organic fern structure can be captured by the mechanical process of find-and-replace on textual symbols.

Now that you hopefully understand how L-systems grow, you might ask yourself: what other patterns emerge when I choose a different axiom and rules? I created an interactive example so you can find out for yourself! Enter your own axiom and rules and the resulting image will automatically be drawn. There are 10 symbols with visual interpretations that are provided in the table below. Play around and see what you can create! If you want some inspiration, you can click on the presets to autofill the inputs with some famous examples of L-Systems.

A Bigger Picture

At this point, you might agree that L-systems are fun mathematical toys, and that they can generate beautiful and complex structures. While this is true, there are deeper and more interesting things left to uncover! Going forward, we will use L-systems as an analogy to explore an area of math which deals with near-philosophical ideas like truth, proof, and meaning.

As we start down this new path, let's look at L-systems from a different perspective. Previously, we started from an axiom and rules and used this to generate an image. Now, let's reverse the process. Imagine that I show you a picture of an L-system and ask you to figure out the axiom and rules that generated it. You can imagine that the L-system is a miniature world. You observe the visual features of the L-system, which gives you some intuition about how it behaves. The task of finding an axiom and rules that generate the L-system is like finding a set of laws that govern its world, generating the picture you observe.

You can compare this to the process of discovering the laws of physics. Early physicists observed our world and noticed certain behaviors, like the tendendency of objects to accelerate down to Earth. They formulated the laws of gravity to explain this observation. The common idea here is the process of finding a core set of information to capture observed behaviors.

So how does this connect to the realm of pure mathematics? In math, we often begin with intuition. For example, we know how to add and subtract numbers because we understand the concept of giving and receiving objects or money. Our intuition about addition and subtraction is like a "picture of arithmetic" that we have in our heads. While intuition is great, mathematics is all about precision and rigor (more on this later). So we want to find a core set of of truths (the axioms) and some rules of inference which can be used to deduce the facts about arithmetic that we intuitively have in our heads.

In the case of arithmetic, the following set of axioms turns out to be sufficient to prove every familiar fact about the natural numbers:

These are called the Peano axioms. Assuming only these 5 axioms to be true, we can use logical rules of inference to prove all theorems about the natural numbers. We can reconstruct a picture of arithmetic.

Let's consider an intuitive fact about the natural numbers, 1 ≠ 2 and let's verify that we can prove this fact from our axioms. In other words, let's pretend that we know nothing about math besides the 5 Peano axioms above, and build a logical argument to show that 1 ≠ 2. Here is a proof:

This may seem like a silly example, but we can prove much more interesting facts too. It might take a long time to fully write and explain the proofs, but it's certainly possible!

Why Proofs?

So why do we even need proofs in the first place? Isn't it kind of tedious to go through multiple logical steps to prove something super obvious like 1 ≠ 2?

Well, yes it is tedious, but it's also worthwhile. At first, it's important to develop an intuitive understanding of mathematical concepts in relation to the real world. But as you begin to consider more complex concepts, intuition can fail us. This is where a proof built from the axioms provides confidence that a non-obvious statement is true. Some of the most beautiful and interesting theorems in math are highly non-intuitive, but we know they are true because they arise as a logical consequence of simple assumptions via proof.

Proofs are especially important in research, at the frontier of math. In research, mathematicians think about various mathematical objects and ask questions about their properties and behaviors. They don't know the answers! Sometimes, they have a guess, a hypothesis. The only way to confirm or reject their hypothesis, thereby advancing our knowledge of math, is to write a proof.

The Biggest Picture

From arithmetic, to calculus, to linear algebra, mathematicians have come up with axioms for many different theories. But what if we consider an even bigger picture—the picture of all of mathematics? Is there a fundamental set of axioms which captures the behavior of all mathematical structures and objects? Is there a set of axioms from which every mathematical theorem can be derived? Suprisingly, amazingly, awesomely, the answer is yes!

The axioms of set theory (specifically, the ZFC axioms) are enough to generate the entire mathematical universe. Think of any mathematical object. Its behaviors are encapsulated by these axioms. Imagine any mathematical theorem. You can prove that theorem from these axioms. Woah.

So what are these fundamental truths so powerful that all mathematics can be derived from them? They are surprisingly simple. To go in depth into each axiom would require some additional background information about set theory and logic. But at their core, the axioms of ZFC are 9 statements that describe the properties of mathematical objects known as sets. A set is simply an unordered collection of items, with no repeats. Sets are commonly written with curly braces. For example, the following are sets:

Note from the last example that sets can contain other sets as their elements. Sets can also be infinite, for example the collection of natural numbers {0, 1, 2, 3, 4, ...} is a set.

But what's really mind blowing is that in the world of set theory, we ONLY assume basic information about the behavior of sets. We begin without even having the concept of numbers. So at first, we can't even talk about the set {1, 2, 3} because the axioms don't define what 1, 2, and 3 mean.

How do we derive theorems about numbers, operations, functions, or literally anything besides sets? It turns out that any mathematical object we can conceive can be modelled as a set. Specifically, some complex set of sets of sets of sets. At the innermost level of these nested sets, every set is empty. The behaviors of all mathematical objects are then simulated by the simple properties of the constituent sets that they are composed of.

For example, the natural number zero is defined as:

And the successor of a natural number is defined as the set which includes everything in the previous set, plus the previous set itself. So we get:

Once we define the natural numbers in this way, we can prove from the axioms of set theory that these natural numbers satisfy the 5 Peano axioms, so they can be used to prove any familiar fact about the natural numbers. We have generated the picture of arithmetic. In much the same way, we can reconstruct ANY mathematical object (functions, real numbers, complex numbers, and anything else you can imagine) out of sets such that the properties of the constituent sets work together to simulate the behavior of the object as a whole. This is how the axioms of set theory generate the picture of all mathematics.

An Incomplete Picture

We've come a long way from where we started. At first we considered L-systems, which generated pictures from an axiom and rules. Then, we turned to the world of pure mathematics and explored how different fundamental truths (axioms) could be combined with logical deduction systems (rules) to generate "pictures" of mathematical theories like the theory of arithmetic. Finally, we learned that some sets of axioms (like the axioms of set theory) are powerful enough to generate the picture of ALL mathematics.

As we come to the end of our journey, lets think a little bit more deeply about the idea of a "picture of all mathematics." What does it mean to be able to generate such a picture?

Intuitively, it should mean that if a mathematical statement is true, then we can prove that statement from our axioms. Furthermore, the reverse should be true: if we can prove a statement from our axioms, then that statement should be true. The first property is often called completeness while the second is called consistency.

At this point, I have to admit that I lied a little bit, because it turns out that under this definition the axioms of set theory cannot generate the picture of all mathematics. Specifically, assuming that set theory is consistent, there are some true mathematical statements that can never be proven from its axioms. So why not just add new axioms, or choose a better set of axioms that generates the complete picture?

It turns out that this is impossible, as proven by mathematician Kurt Gödel in his famous Inconsistency Theorem. No matter what axioms we choose, there will always be parts of the picture of mathematics that remain in shadow. I find this fact to be simultaneously unsettling and incredible. It feels uncomfortable that there exist mathematical questions that we can never answer. But that is also exactly what fills me with wonder and reverence for mathematics and the beauty of the great unknown.