Undefined Behavior

exploring expression through mathematics and code

Mathemusic

by Eric Chen

When you listen to music, each note has a certain frequency which governs how "high" or "low" it sounds. As you ascend the piano chromatically (which means to increase one note at a time, including the black notes) you can hear the frequency rising steadily higher.

Based on what you hear you might think that the frequency of the notes is increasing linearly. If we were to plot the frequency of each note on a graph you might expect to see something like this:

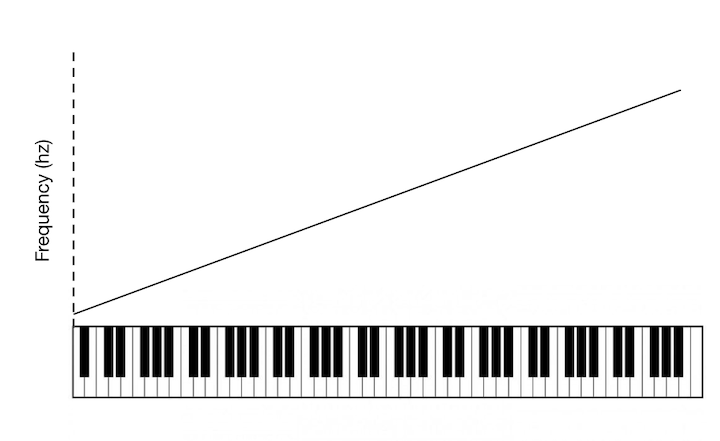
a graph depicting a linear relationship between notes on a keyboard and frequency in hertz

But that would be inaccurate. As it turns out, frequency increases exponentially as you climb chromatically. So the true picture looks something like this:

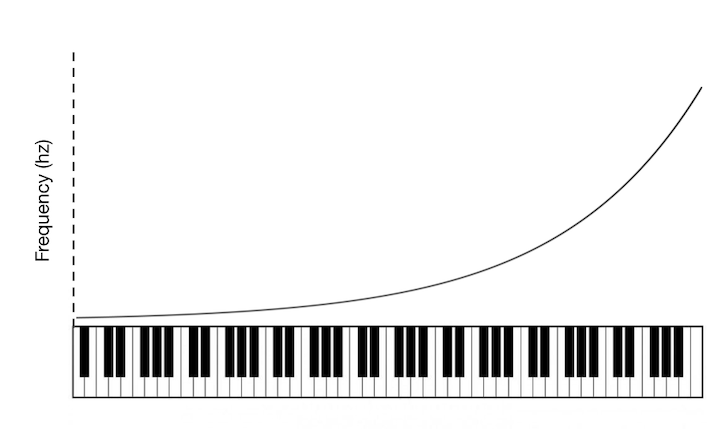
a graph depicting an exponential relationship between notes on a keyboard and frequency in hertz

In other words, moving up by one note (which is called moving up a half step) corresponds to multiplying by a constant frequency ratio, rather than adding a constant frequency difference.

As an aside, frequency ratios form the basis for the theory of harmony. For example, doubling the frequency of a note preserves its "pitch class," leaving it as the same note, only higher. Various other ratios besides the 2:1 ratio for the octave exist which create unique sounds. These are called intervals and they are stacked together to create chords.

When I realized that my initial intuition about frequency was wrong, I started to wonder what would happen if the relationship between notes and frequency really was linear rather than exponential. What would music sound like? Furthermore, what if we tried using other functions like polynomials or logarithms? In an effort to find out, I wrote some Python code that takes a function as input and re-maps the frequencies of a music file according to the function.

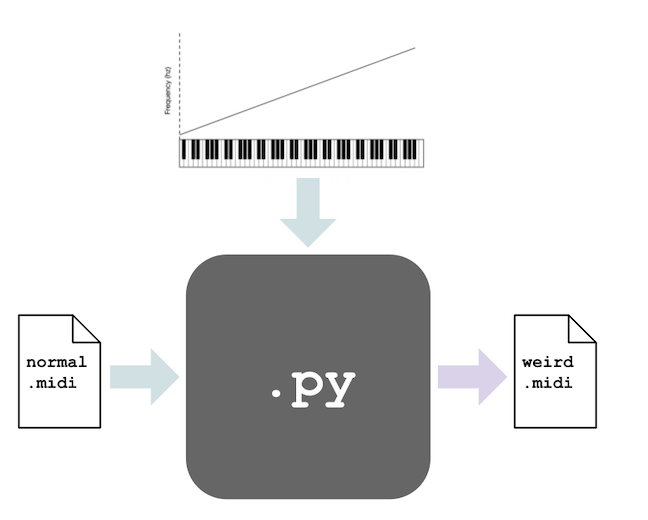
a normal midi file and a function are fed as input into a Python script to output a new, transformed midi file

With this tool in hand, I could dream up any function and then listen to how that choice affected a familiar piece of music.

Linear Frequency Function

The first thing I experimented with was a linear function. Here is what chromatically ascending on a piano sounds like with a linear frequency function.

Weird, right? The notes sound like they increase by large jumps at the beginning and then smaller jumps as the pitch gets higher. Why might this be?

Think back to our initial observation: our ears perceive an exponential frequency increase as a linear frequency increase. From this observation, we can infer that our ears hear in log-frequency. In other words, our perception of pitch is aligned with the logarithm of the frequency function, rather than the frequency function itself.

Now our frequency function is linear, so our log-frequency function (what our ear perceives) is a logarithmic function. This explains why our chromatic ascent sounds like it makes large jumps at the beginning and smaller jumps as the pitch gets higher: that is exactly how a logarithmic function increases.

Having heard the weird sounding chromatic ascent with the linear frequency function, I was eager to try it out on a complete song. Here is the regular version of the song Fur Elise, which you might recognize:

And here is Fur Elise with a linear frequency function:

When I heard this for the first time I literally cried with laughter because it sounded so ridiculous! It is really interesting to me how the mood of the song has totally changed from somber and beautiful to something weirdly spooky and alien and absurd.

Quadratic Frequency Function

Now what if we mapped frequency to some other function besides a linear one? For example, what if we used a parabola?

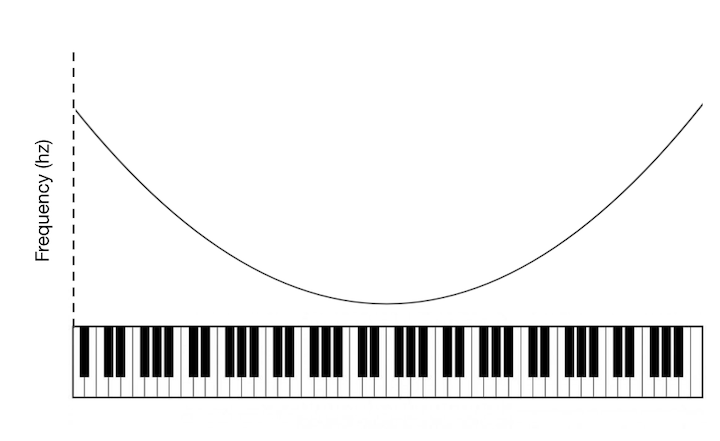
a graph depicting a quadratic relationship between notes on a keyboard and frequency in hertz

Let's start with the chromatic ascent again. Here is what it sounds like with the quadratic frequency relationship:

It doesn't really sound like an "ascent" anymore since the quadratic function is not monotonically increasing. The pitch decreases and then increases again as we climb up the piano. This is what Fur Elise sounds like under this frequency mapping:

Once again the vibe of the song is totally unrecognizable! This one makes me think of some shady and suspenseful scene from a spy movie.

More Fun to be Had

Obviously, there are an infinitude of other functions we could try. The functions don't even have to be continuous. (Since we only need to assign some frequency value to each of the 128 discrete MIDI note values.) There are so many possibilities to experiment with this further!

Another really cool idea would be to allow a user to draw their own line over a piano diagram, and have that line define the frequency mapping. I hope to create this as an interactive example soon. Looking even further ahead, it would be amazing if this idea could be built into a real-time instrument which changes the frequency function according to the performer's hand-motions.